10/9/2014 Impulse Momentum Activity

Purpose:
This lab purpose is to find the objects impulse which is applied to an objects that equals the change in momentum of that object. To do this we will use two carts to measure the force impact and the velocity of the cart.

Experiment:
In this lab we set up a cart attached to a pole so we could use the spring it has inside the cart to measure impact with another cart which has a force sensor. So the moving cart will collide into the station cart with the spring and allows the initial cart to be pushed back after the collision. During the collision we measure the non constant force and the carts non constant velocity before during and after the impact. Here is a picture of the experiment.

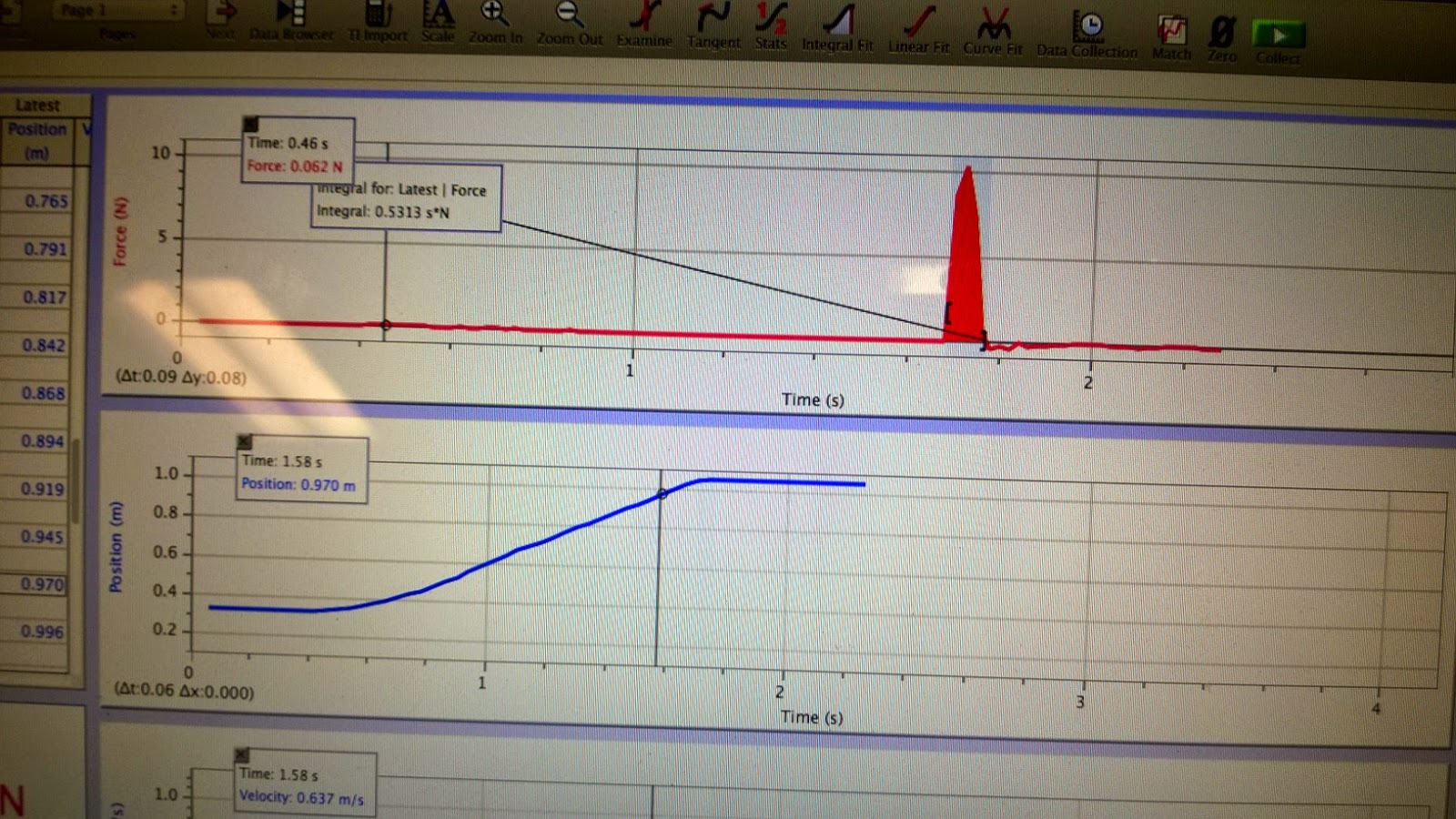
Here is the data of the force, position, and velocity of the moving cart which is the blue cart in the picture being pushed and bouncing back. Are force sensor is reading a negative force in this picture, but we reverse the sensor and repeated the experiment. As you can see the collision is less than 1/5th of a second.

Now that we have the data collected we can calculate the impulse of the carts collision by taking the integral of the change in Force respect to time from begging of collision to the end(momentum). We repeated the experiment against with the force being positive then increased the mass of the car and did the experiment again. The integral of the momentum is simply the area under the graph as shown below.

M = 403 grams

With our own calculations we have:

m = 403 g

Vo = 0.48 m/s

Vf = -0.38

m(Vf - Vo) = Impulse

0.403(-0.38 - 0.48) =  -0.346

M = 803 grams

With our own calculations we have:

m = 803 g

Vo = 0.633 m/s

Vf = -0.5

m(Vf - Vo) = Impulse

0.803(-0.5 - 0.633) =  -0.907

Both experiments our signs where wrong but this is because we flipped the force sensor sign and not the position sign.

The next part of the impulse lab we used a clay block instead of a cart with a spring for the impact object. So now when the cart collide it will stick into the clay and not bounce back. Here our the graphs. You can see in the data collection the position does not change back and the velocity stops suddenly so the energy is not conserved. The integral Force respect of time to find the impulse of the impacts.

Mass 403 grams

Mass 803 grams